Recursions and PHP
Introduction
Recursion occurs when something uses a similar version of itself. Recursive procedure is one where at least one of its’ steps calls for a new instance of that very same procedure (broadly speaking we say that function calls itself). It is similar to iteration, with one major difference – iteration requires predefined number of repetitions, and with recursion one doesn’t need to know in advance how many repetitions there will be. In order to limit the number of repetitions and to avoid or stack overflow there must be a terminating scenario defined, so that the procedure can complete.
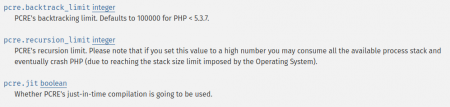
PHP limits the number of recursive calls and but it’s possible to expand this limit in php.ini file options.
http://php.net/manual/en/pcre.configuration.php
All recursive algorithms must have the following:
1. Base Case – end condition which is the solution to the “simplest” possible problem
2. Work toward Base Case – making the problem simpler
3. Recursive Call – using the same algorithm to solve a simpler instance of the problem
In order to show on a simple example how recursion works we will use the factorials. In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n. For example: 5! = 5 * 4 * 3 * 2 * 1 = 120. Let’s write two simple algorithms to calculate the factorial value of given integer.
The first example will use iterative approach:
$number = 5;
function iterativeFactorial($number)
{
if ($number < 0) {
return -1; //initial condition, if number is negative exit the program
}
else if ($number === 0) {
return 1; //factorial of 0 is 1
}
$factorial = 1;
if ($number <= 1) return $factorial;
while ($number > 1) {
$factorial *= $number;
$number--;
}
return $factorial;
}
The second example will use recursive approach:
$number = 5;
function recursiveFactorial($number)
{
if($number < 0) {
return -1; //initial condition, if number is negative exit the program
}
else if($number === 0) {
return 1; //base case to exit the recursion
} else {
return $number * recursiveFactorial($number-1); // recursive call
}
}
How It works
Phase One – creating new instances and saving them on stack
This phase is characterized by creating new instances of function calls and storing them on stack together with their addresses. In the first call the variable equals to 5 ($number = 5). It goes through initial condition – number must be positive in order to continue down the function. Then the base condition in which if number equals to zero the function will exit recursion. If this doesn’t happen ($number > 0), the function will call itself recursively to derive new instance of itself – 5 * recursiveFactorial( 5 – 1 ). The first instance of the function will wait on stack while the new instance repeats the process, this time $number variable will be equal to 5 – 1, which is 4 and it will compute 4 * recursiveFactorial (3). The process will continue until the $number variable is zero, in which case the function will return 1 and won’t call for the new instance of itself (base condition). At this point all created instances are waiting on stack, together with their return addresses.
Phase Two – Computing and deleting created instances from stack
The returning of 1 wakes up the last created instance of the function on stack (the one that called It – $number = 1), which accepts the return value of 1 and uses it to compute 1 * recursiveFactorial(1-1). This returns 1, the called instance is being deleted from stack and the next instance on stack is being called ($number = 2). After computing 2 * recursiveFactorial(2-1), 2 is returned, the called instance is being deleted from stack and next instance on stack is being called. The process continues until the “oldest” instance of function (the first one to be stored on stack, $number = 5) is computed and the final value of 120 returned.
Simple test
Both functions were ran as php files from command line, using Ubuntu on my laptop. The $number variable was set to 150 and each function was ran 3 times. The results showed that on average recursive approach needed approximately 3.7 times more time than iterative.
Conclusion
The main disadvantage of recursive approach is that the algorithm may require large amounts of memory if the recursion goes very deep. This is because when the function is called, a new instance is created in memory. Also, it will most likely consume more time than iterative. Both disadvantages can be minimized with tail optimization which is not supported in PHP.
However there are pros to using recursive approach. It is more elegant and makes code more readable. Because of that it can reduce time needed to write and debug code. This approach is more suitable for solving specific problems, when problem can be broken down into smaller pieces (such as sorting algorithms).
The ultimate goal should always be to get as close as possible to achieving ‘low memory consumption and short execution time’. It’s up to a programmer to decide which approach works better for a specific problem in a specific development environment.